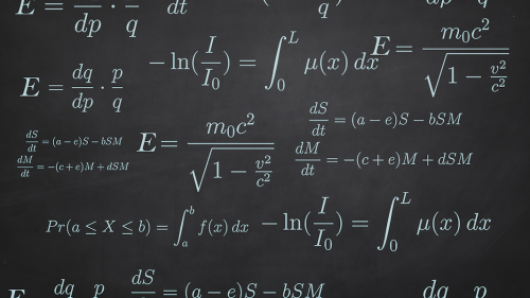Multivariable Calculus
Image

Pace
Instructor-led
Subject
Course Language
English
Video transcript
English
Intermediate
Platform
Extension School, Harvard Division of Continuing Education
Associated Schools