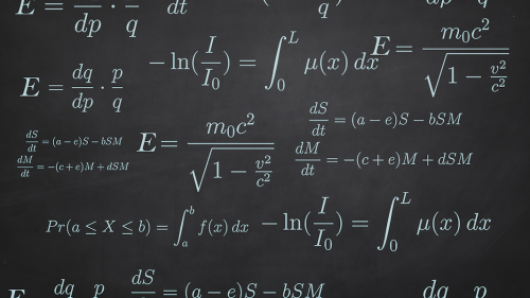Professional and Lifelong Learning

Course description

Complex analysis is the study of functions of a complex variable. A complex variable (z) can take on the value of a complex number (x + iy), where i is the unit imaginary number and x and y represent real numbers. Differentiation and integration of complex functions involve procedures used to differentiate and integrate functions of real numbers. Thus, if you enjoyed calculus of real variables, you would enjoy complex analysis. During the semester, we discuss limits, continuity, differentiation, and integration involving exponential, logarithmic, power, trigonometric, hyperbolic, inverse trigonometric, and inverse hyperbolic complex functions. Cauchy-Riemann equations, analytic functions, harmonic functions, Cauchy-Goursat theorem, Taylor series, Laurent series, and Cauchy's residue theorem are also discussed.